Zum diesjährigen German Testing Day am 4. Mai war Andreas eingeladen, mit einem Vortrag sein Know-how an interessiertes Fachpublikum weiterzugeben. Wir haben seine Ausführungen nun noch einmal in einem Blogartikel aufgegriffen und wollen euch ausführlicher beschreiben, wie ihr mittels künstlicher Intelligenz eine „Fehlerauftrittswahrscheinlichkeit“ ermitteln könnt. Achtung, es wird anspruchsvoll!
Intro
Markus ist frustriert. Ihm bleiben noch zwei Tage Zeit, bis das neue Release ausgeliefert werden muss. Und erst gestern Abend wurde die Version ins Testsystem eingespielt. Sein Blick streift über die 582 Testfälle, die im Test-Management-Tool angelegt sind. Um alle Tests durchzuführen, wären fast 150 Stunden Arbeitszeit einzuplanen. Und dann ist der zweite Tester auch noch zu einem Parallelprojekt abgerufen worden…
„Wenn es doch eine Glaskugel gäbe, die mir vorab sagen könnte, welche Tests wohl einen Fehler finden werden“, seufzt er und beginnt mit der Arbeit.
Eine Glaskugel kann ich leider nicht bieten – jedoch ein mathematisches Modell, um die Glaskugel zu modellieren. Dieses Modell besteht dabei aus drei Schritten:
- Erfassen von Metriken, basierend aus Daten der Vergangenheit für jeden einzelnen Testfall
- Berechnung einer „Fehlerauftrittswahrscheinlichkeit“ für jeden einzelnen Testfall
- Priorisierung der Testfälle anhand der „Fehlerauftrittswahrscheinlichkeit“

Schritt 1: Der Blick in die Vergangenheit
Konfuzius wird dieses Zitat zugeschrieben: „Erzähle mir die Vergangenheit, und ich werde die Zukunft erkennen.“ Ohne diese Erfahrungswerte bleibt für eine Priorisierung der Testfälle nur die Option „Bewertung anhand abgedeckter Produktrisiken“ oder gar „Zufällige Auswahl“. Sind hingegen Informationen vorhanden, welche Bereiche der Software besonders häufig FAILED waren, kann dies ein guter Indikator sein, der die Priorisierung von Testfällen beeinflusst.
Doch was heißt hier „Erfahrung“ bzw. „Information“? Welche Metriken können herangezogen werden?
In der Literatur finden sich u.a. die folgenden Metriken:
| Metriken für manuelle und automatisierte Tests | Beschreibung | Annahme |
| Letztes Ergebnis | Letztes Testergebnis | Der Fehler wird jetzt wieder auftreten. |
| Fehlerrate | Fehlerrate über die letzten N Testläufe | Häufige Fehler in der Vergangenheit werden häufiger in der Zukunft Fehler zeigen. |
| Testdauer | Dauer des letzten Testlaufs | Längere Tests werden mehr Fehlerzustände erkennen. |
| Datum des Testfalls | Datum der Testfall-Erstellung | Neuere Tests werden neue Funktionalitäten testen. |
| Einzigartigkeit des Testfallnamens | Cosinus-Ähnlichkeitsmaß, so dass Tests mit möglichst unterschiedlichen Namen bevorzugt werden („test1(), test2(), ganzAndererName()“) | Tests mit ähnlichem Namen werden ähnliche Bereiche abtesten. |
Für automatisierte Tests sind noch folgende zusätzliche Metriken relevant:
| Metriken für automatisierte Tests | Beschreibung | Annahme |
| Code Coverage Metriken | Abdeckung des Codes, bspw.: Line Coverage Function Coverage CK Metriken Branch Coverage Zyklomatische Komplexität | Komplexer Code wird zu häufigeren Fehlern führen. |
| Änderungsrate | Änderungsrate des Tests bzw. des getesteten Programmcodes | Häufig geänderter Code wird zu häufigeren Fehlern führen. |
| Critical Sections | Anzahl der Testfälle, die den gleichen Codeabschnitt mit mehreren Tests unterschiedlich testen | Bereiche, die mit vielen Tests abgedeckt sind, sollten verstärkt getestet werden, da sie kritische Logik enthalten. |
Schlussfolgerung: Wir benötigen eine Datenbank, um Daten aus der Vergangenheit zu speichern.
Schritt 2A: Der Blick in die Zukunft
Wir erinnern uns: Die Aufgabe der Glaskugel ist es, VOR der Ausführung eines Testfalls zu bestimmen, welche Testfälle NACH der Ausführung das Ergebnis „Failed“ haben werden. Anders gesprochen: Wir benötigen eine Funktion P(Testfall), um jedem Testfall anhand vergangener Daten eine Wahrscheinlichkeit zuzuordnen, dass dieser Test im nächsten Testlauf wieder „Failed“ sein wird. Zur Vereinfachung nehmen wir an, dass Wahrscheinlichkeiten > 50% der Klasse „FAILED“ zugeordnet werden können.
Nehmen wir an, wir hätten zwei verschiedene Funktionen P1(Testfall) und P2(Testfall), um diese Bewertung vorzunehmen. Gibt es ein Kriterium für die Unterscheidung, welche Funktion die „Zukunft“ besser beschreiben kann beziehungsweise welche Vorhersage tatsächlich eingetroffen ist?
Auch hier hilft der Blick in die Literatur, in der die Metrik „Average Percentage of faults detected (APFD)“ beschrieben wird.
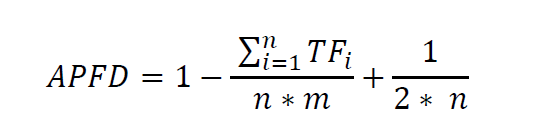
n = Anzahl der Tests
m = Anzahl der aufgetretenen Fehler
TFi = Position des i-ten Fehlers
Die Aufgabenstellung der Testpriorisierung wird damit zu einer Optimierungsaufgabe, die sich wie folgt beschreiben lässt: „Finde eine Funktion Px(Testfall) dergestalt, dass der Wert von APFD maximiert wird.“ Diese Funktion Px(Testfall) ist also gleichbedeutend mit unserer „Glaskugel“.
Schlussfolgerung: Die Bestimmung der Fehlerauftrittswahrscheinlichkeit kann als Optimierungsfunktion aufgefasst werden – und ist wie bei vielen Optimierungsaufgaben nicht eindeutig lösbar.
Schritt 2B: Auswahl der verwendeten KI-Verfahren
Um eine sinnvolle Beschreibung der Funktion Px(Testfall) zu erhalten, betreten wir das weite Feld der Verfahren des maschinellen Lernens. Für diese Aufgabenstellung haben wir uns für die folgenden vier Verfahren entschieden, die typische Vertreter des maschinellen Lernens sind:
- Support-Vector-Machine
- Neuronales Netz
- K-Nearest Neighbour
- Hoeffding-Tree
In einem ersten Schritt wurde die Performance der verschiedenen Verfahren verglichen. Dabei wird ein Testset mit N Durchläufen simuliert, wobei zirka 25% der Tests FAILED pseudo-zufällig gehen werden. Die Eingangsdaten für die neuronalen Netze basierten auf den oben genannten Metriken.
In der folgenden Grafik sind die dabei erreichten Klassifikationsergebnisse zusammengefasst. In der x-Ache ist die Anzahl der Testläufe dargestellt, in der Y-Achse die Anzahl der so korrekt vor-klassifizierten Testfälle.
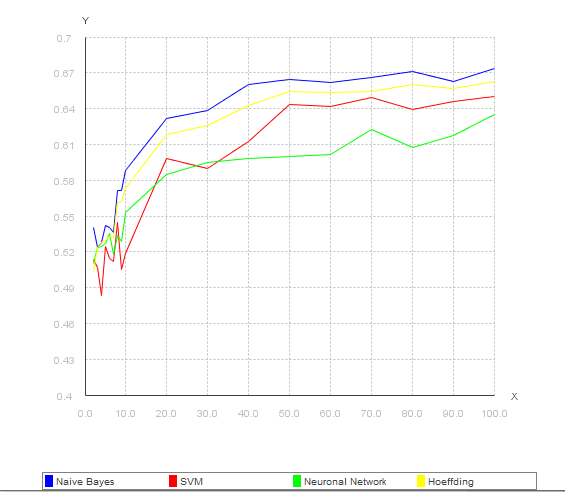
Zwei Erkenntnisse ergeben sich aus dieser Darstellung:
- Alle Verfahren sind in der Lage, die Wahrscheinlichkeit Px(Testfall) zu berechnen.
- Bereits nach 15 bis 20 Ausführungen eines Testsets ist keine Steigerung der Erkennungsrate zu verzeichnen.
Für den praktischen Einsatz gibt es neben der reinen Klassifikation noch einen zweiten Baustein zu beachten: Bei der Testpriorisierung ist kein Training anhand von Testdaten möglich. Gewünscht ist, dass die Klassifikation „on the fly“ mitlernt, das Training also inkrementell erfolgen muss. Der Hoeffding-Tree bietet hier den Vorteil, dass er bereits mit seiner Algorithmik die Möglichkeit des inkrementellen Lernens unterstützt.
Schlussfolgerung: Für die Aufgabenstellung des inkrementellen Lernens eignet sich ein Entscheidungsbaum hervorragend.
Schritt 2C: Auswahl der Tests
Dieser Schritt lag aktuell nicht im Fokus der Analyse und kann perspektivisch deutlich umfangreicher ausfallen. Hier können wir uns die folgenden Metriken vorstellen, um die tatsächliche Selektion zu beeinflussen:
- Zur Verfügung stehende Zeit (Welche Tests sollen ausgeführt werden, wenn ich die Erwartungswerte von Testdauer + Fehlerauftrittswahrscheinlichkeit kenne?)
- Durch die Tests abgedeckte Produktrisiken (Welche Tests decken kritische Geschäftsbereiche ab und sollten bevorzugt ausgeführt werden?)
- Geänderte Codebereiche (Welche Tests sollen priorisiert werden, wenn berücksichtigt wird, an welchen Stellen Änderungen zur letzten Version aufgetreten sind?)
- Anzahl der Tests (Wähle die 20% aus allen Tests, bei denen in der Vergangenheit besonders häufig Fehler gefunden wurden!)
Zur Vereinfachung haben wir uns entschieden, die Testfälle nach ihrer „Fehlerauftrittswahrscheinlichkeit“ absteigend zu sortieren.
Schlussfolgerung: Die Auswahl der Tests ist Gegenstand der weiteren Entwicklung und kann unabhängig von der Berechnung der Fehlerauftrittswahrscheinlichkeit erfolgen.
Schritt 3: Praktische Umsetzung mit TestNG + JaCoCo – der „CurrantRunner“
Der beschriebene Ansatz, die Reihenfolge der Testfälle basierend auf den Ergebnissen der Vergangenheit zu ändern, haben wir in eine Bibliothek integriert. Der Code ist dabei als OpenSource auf GitHub verfügbar (https://github.com/proficomde/CurrantRunner, Beispiel-Projekt: https://github.com/proficomde/CurrantRunner_Examples).
Der Toolstack basiert aktuell auf Java und TestNG, wobei die Testklassen mittels JaCoCo instrumentiert werden. Die Klassifikation wurde mit dem WEKA-Framework vorgenommen.
Zur Nutzung ist in der pom.xml folgender Eintrag notwendig:
<parent>
<groupId>de.proficom.currantrunner</groupId>
<artifactId>currantrunner-testng-maven</artifactId>
<version>1.0</version>
</parent>Während der Ausführung der Tests (Maven: mvn test) werden dabei verschiedene Metriken erfasst und in einer Datenbank erfasst. Ab dem zweiten Testlauf wird dann die Reihenfolge der Tests wie in den Abschnitten zuvor angepasst, um kritische Testfälle zuerst auszuführen.
Anzumerken ist, dass der beschriebene Algorithmus und die aktuelle Implementierung so generisch angelegt sind, dass perspektivisch auch andere Test-Frameworks wie JUnit oder auch die Ergebnisse von manuellen Tests als Eingabedaten denkbar sind.
Zusammenfassung und Ausblick
Die Aufgabenstellung, potenzielle Tests auszuwählen, die das Testergebnis FAILED aufweisen werden, ist prinzipiell mit Methoden der KI lösbar. In unseren Simulationen hat sich der Hoeffding-Tree als wirkungsvoller Algorithmus gezeigt. Prinzipiell eignet sich dieser Ansatz dabei sowohl für automatisierte als auch manuelle Tests.
Die Frage, welche Metriken in welchem Kontext (manuelle Tests, automatisierte Tests, …) sinnvoll einsetzbar sind, muss noch anhand realer Testdaten evaluiert werden.
Der CurrantRunner ist als OpenSource-Projekt verfügbar und kann für weitere Experimente und Entwicklungen genutzt werden.



